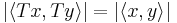Wigner's theorem
Wigner's theorem, proved by Eugene Wigner in 1931,[1] is a cornerstone of the mathematical formulation of quantum mechanics. The theorem specifies how physical symmetries such as rotations, translations, and CPT act on the Hilbert space of states.
According to the theorem, any symmetry acts as an unitary or antiunitary transformation in the Hilbert space. More precisely, it states that a surjective map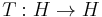 
on a complex Hilbert space 
that satisfies
for all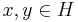 
has the form 
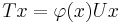for all 
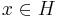, where 
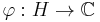has modulus one and 
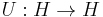is either unitary or antiunitary.
Symmetry in quantum mechanics
In quantum mechanics and quantum field theory, the quantum state that characterizes one or more particles or fields is a vector (ket) in a complex Hilbert space. Any symmetry operation, for example "translate all particles and fields forward in time by five seconds", or "Lorentz transform all particles and fields by a 5 m/s boost in the x direction", corresponds to an operator T on that Hilbert space. This operator T must be bijective because every quantum state must have a unique corresponding transformed state and vice-versa. Also, the probability of finding a system in state 
when it is initially in state 
is given by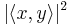 
. Since T is a symmetry operation, the probability of finding the system in state 
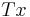when it is initially in state 
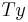must be the same; therefore 
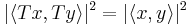. It follows that T satisfies the hypotheses of Wigner's theorem.
Thus, according to Wigner's theorem, T is either unitary or anti-unitary. In the two examples above (time translations and Lorentz boosts), T corresponds to a unitary symmetry operator. The time-reversal symmetry operator is a famous example of an anti-unitary symmetry operator.
References
- ^ E. P. Wigner, Gruppentheorie (Friedrich Vieweg und Sohn, Braunschweig, Germany, 1931), pp. 251-254; Group Theory (Academic Press Inc., New York, 1959), pp. 233-236
- Bargmann, V. "Note on Wigner's Theorem on Symmetry Operations". Journal of Mathematical Physics Vol 5, no. 7, Jul 1964.
- Molnar, Lajos. "An Algebraic Approach to Wigner's Unitary-Antiunitary Theorem". arXiv:math/9808033